【算法】浅谈K-D Tree&学习笔记

又是一个神奇的数据结构……

$K$-$D \ Tree$ 中 $D$ 是维度($Dimension$)的缩写，所以 $K$-$D \ Tree$ 的实际意思就是 $K$ 维树。当然 $K$-$D \ Tree $ 一般用于维护二维平面上的信息，所以我们平常用的 $K$-$D\ Tree$ 又叫 $2$-$D \ Tree$ 。

假设我们现在有一个二维平面，二维平面上有若干个点，现在怎么用 $2$-$D \ Tree$ 维护这些点呢？很简单，我们将这些点建成一颗树，最好是一颗二叉搜索树，但是怎么建树呢？我们就来分割这个平面，横着一刀，竖着一刀，每次选取最优的结点当根即可。

可能很抽象，我们以下图为例，假设我们需要将下图的 $7$ 个点建成二叉搜索树：

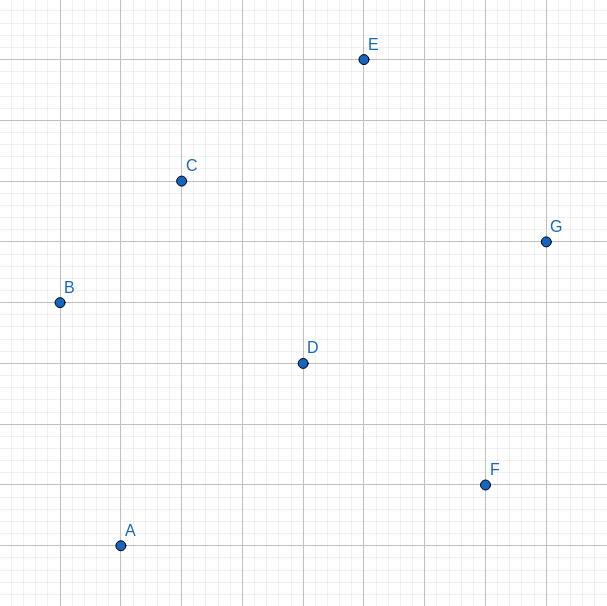
首先我们准备竖着切，这个竖着切切哪里呢？我们会发现 $D$ 是最中间的结点，于是我们对着 $D$ 就是一刀，现在的矩阵分割成了两半，那么自然的 $A,B,C$ 就是 $D$ 的左子树中的结点，$E,F,G$ 就是 $D$ 的右子树中的结点。

然后我们先建 $D$ 的左子树，由于上一次是竖着切的，这一次我们需要横着切。我们递归下去，发现 $A,B,C$ 这一块 $B$ 是最中间的(以横着的视角，因为需要横着切嘛)，那么很显然 $D$ 的左儿子就是 $B$ 了，$A,C$ 分别是 $B$ 的两孩子，由于 $A,C$ 已经在 $B$ 的左右了并且只有一个点了，那么理所当然 $C$ 就是 $B$ 的左孩子，$A$ 就是 $B$ 的右儿子(横着看就好了)。

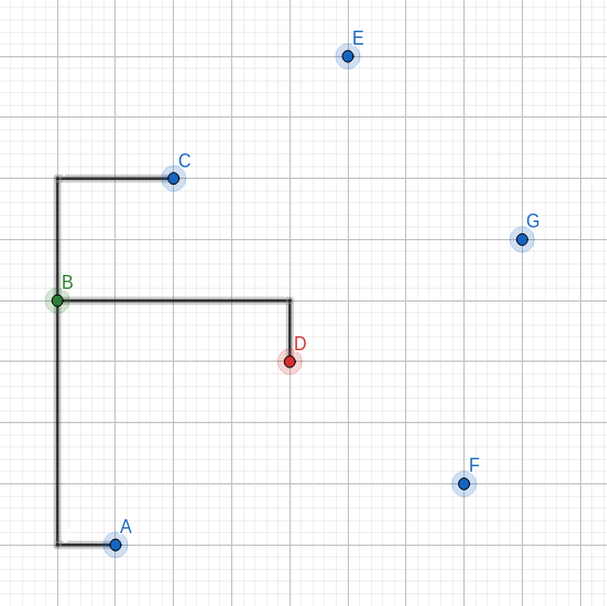
同样的，我们发现 $G$ 是 $D$ 左边横着切时最合适的结点(因为在横着的视角中 $G$ 是最中间的 )，于是我们将 $D$ 的右儿子定为 $G$ ，同样的，$F,E$ 为 $G$ 的两孩子。

那么这样子我们的树就建好了。

Code-build-kdt:

int build(int l,int r,int wd) {//lr:当前对应的结点区间,wd:当前需要切的方向
    if(l>r) return 0;
    int x=new_node(),mid=(l+r)>>1;//新建结点
    WD=wd,nth_element(p+l,p+mid,p+r+1),//重载了运算符，按照当前切的方向排序
    tr[x].tp=p[mid];//找到最合适切割的最中间的结点
    tr[x].l=build(l,mid-1,wd^1);//建立左子树
    tr[x].r=build(mid+1,r,wd^1);//建立右子树
    return pushup(x),x;//上传信息
}

但是怎么查询呢？实际上查询跟普通的二叉搜索树差不多，按照方位坐标查找即可。

对于一个结点的信息是这样的：

Code-node-kdt

struct node {
    int mi[2],mx[2],l,r,sz;
    point tp;
}tr[N];

l,r,sz 就是左右儿子以及子树大小，point 显然是该结点代表的二维平面上的点，但是 $mi,mx$ 是干什么的呢？我们用 $mi,mx$ 记录的就是当前结点已经它的子树中的所有节点中，最大/最小的 $x$ 坐标以及最大/最小的 $y$ 坐标。

这样记录有什么用呢？假设我们将这个看成一个矩形，那么对于一个我们需要搜索的坐标，如果这个需要搜索坐标已经不属于 $mi,mx$ 围城的矩阵中，那么这个需要搜索的坐标就跟当前子树没关系了，这也就相当于一个剪枝。

我们的 $pushup$ 上传时就是对 $mi,mx$ 进行更新，所以 $pushup$ 应该这样写：

Code-pushup-kdt

inline void pushup(int x) {
    int l=tr[x].l,r=tr[x].r;//简写左右儿子
    tr[x].sz=tr[l].sz+tr[r].sz+1;//更新size
    for(int i=0;i<=1;++i) {//枚举方向，节省码量
        /*---------更新mi[x],mx[x]---------*/
        tr[x].mi[i]=tr[x].mx[i]=tr[x].tp.x[i];
        if(l) {
            tr[x].mi[i]=min(tr[x].mi[i],tr[l].mi[i]);
            tr[x].mx[i]=max(tr[x].mx[i],tr[l].mx[i]);
        } 
        if(r) {
            tr[x].mi[i]=min(tr[x].mi[i],tr[r].mi[i]);
            tr[x].mx[i]=max(tr[x].mx[i],tr[r].mx[i]);
        }
        /*---------更新mi[x],mx[x]---------*/
    }
}

然后呢，这里不待修改的，那么如果说要兹磁插入节点怎么办？

需要兹磁插入节点的题目：[Violet]天使玩偶/SJY摆棋子

这道题因为允许离线，我们可以使用 $CDQ$ ，但是如果强制在线的话就只能用 $K$-$D \ Tree$ 了。我们来讨论 $K$-$D \ Tree$ 的做法。

实际上 $K$-$D \ Tree$ 插入节点非常简单，就像普通的二叉搜索树那样找个位置插就好了。

Code-Insert-kdt

void Insert(point tmp,int&x,int wd) {//tmp:当前需要插入的点,x:当前树中结点,wd:当前切割方向
    if(!x) {//找到要插入的位置了
        x=new_node();//新建结点
        tr[x].tp=tmp,tr[x].l=tr[x].r=0;
        pushup(x);return;
    }
    if(tr[x].tp.x[wd]<tmp.x[wd]) Insert(tmp,tr[x].r,wd^1);//应该往右插
    else Insert(tmp,tr[x].l,wd^1); //否则往左插
    pushup(x);//更新结点信息
}

但是呢，你会发现就像一般的二叉搜索树一样，这个插入很容易被卡，卡成一条链，这就很不舒服了。于是我们需要一些平衡树的思想，使得 $K$-$D \ Tree$ 保持平衡。

“我会 $Splay$ ！我会无旋$Treap$ ！”

呸呸呸，今天我们讲的是替罪羊树，跟你俩没关系。

没错，就是用替罪羊树的思想，将 $K$-$D \ Tree$ 拍扁重建。差不多就是 $insert$ 的时候，在 $insert$ 的最后 $check$ 一下子树是否平衡，如果当前结点的子树已经”不平衡”了，那么拍扁该结点以及该结点子树，重建。

这里的 $\alpha$ 的值一般定为 $0.75$ 左右，但是也不能确定，如果实在要掐得准的话就得看看询问多还是插入多了。不过一般用 $0.75$ 是没问题的。

Code-check&pia-kdt:

void pia(int x,int num) {//就是拍扁的意思,sto litble orz
    if(tr[x].l) pia(tr[x].l,num);//先拍左子树
    p[num+tr[tr[x].l].sz+1]=tr[x].tp,trh[++top]=x;//再拍自己
    if(tr[x].r) pia(tr[x].r,num+tr[tr[x].l].sz+1);//然后拍右子树
}
void check(int&x,int wd) {//判断x的子树是否满足"平衡",wd记录当前切割方向,建树的时候有用
    if(alph*tr[x].sz<tr[tr[x].l].sz||alph*tr[x].sz<tr[tr[x].r].sz)//判断
        pia(x,0),x=build(1,tr[x].sz,wd);//拍扁 and 重新build建树
}

然后就是应用了，值得注意的是，如果维护的不是点而是矩形，那么有些地方(例如边界，$mi,mx$ 都要注意)。

就像这道题：[APIO2018] Circle selection 选圆圈，注意一下细节就好。

本文标题:【算法】浅谈K-D Tree&学习笔记

文章作者:Qiuly

发布时间:2019年03月26日 - 00:00

最后更新:2019年03月30日 - 15:17

原始链接:http://qiulyblog.github.io/2019/03/26/[算法]KD-Tree/

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际转载请保留原文链接及作者。